En esta entrega deduzco la condición de equilibrio de Lagrange para un campo de potencial, que puede o no ser conservativo; es decir univaluado.
Archivo por meses: marzo 2012
Quantum eikonal
En esta entrega encaro el problema de la eikonal cuántica para el caso de la ecuación de Schrödinger en el contexto configuración (1) asumiendo que busco soluciones viajeras (2) resulta la ecuación (5). Esta tiene sentido si la energía mecánica total es mayor a la energía potencial en un punto del espacio. Luego deduzco que forma explícita tiene la eikonal (6) que como se indica en el texto es proporcional a la longitud de camino del rayo. Este detalle produce que la dinámica herede las simetrías del espacio de configuración. Es decir si el espacio tiene simetría esférica, la dinámica lo tendrá.
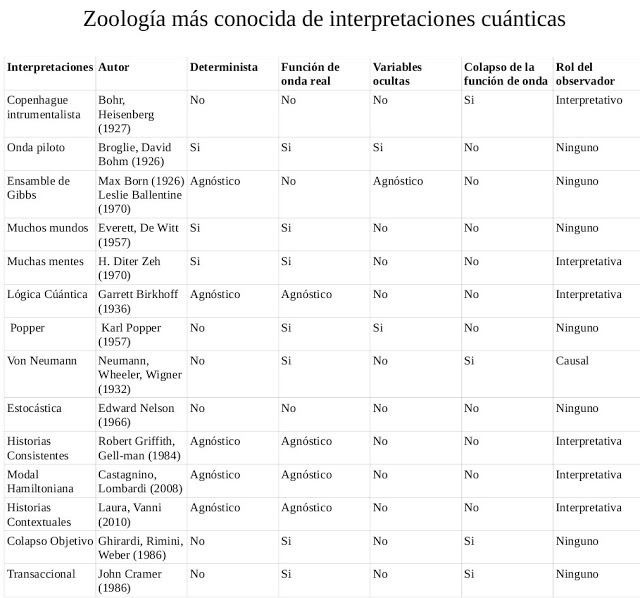
Zoología de interpretaciones cuánticas
La Eikonal en teoría electromagnética
En esta entrega encaro la aproximación de la eikonal (longitud de onda de grupo muy corta o asíntota ultra violeta) de las ecuaciones electromagnéticas (1) bajo la condición de que las fuentes son lejanas y las soluciones son ondas con polarización definida. Bajo la aproximación de la eikonal independientemente de si las ondas son esféricas, planas, etc… los campos responde a las ecuaciones (3) donde la ecuación de la eikonal es (4), esto permite definir lo que son los frentes de onda y por medio de (6) relacionar la eikonal con la longitud de camino óptico. Entonces los frentes de onda son el conjunto de «rayos» con la misma longitud de camino óptico, y viseversa.
La aproximación de la eikonal permite relacional el electromagnetísmo con la óptica geométrica.
Quantum Wootters distance
La distancia de Wootters es una distancia en el espacio de las probabilidades entres dos densidades de probabilidad que tienen el mismo número de valores en su variables discretas (1). Esto permite decir cuando dos procesos son equivalentes en probabilidad, pues su distancia es nula, por (2) se puede extender a la cuántica para definir cuando dos estados son equivalentes respecto de una propiedad (3). En el caso de que dicha propiedad sea el operador configuración resulta (4) con lo cual dos soluciones en la esfera de Riemann son equivalentes aún cuando tengan eikonales diferentes.