SymPy Core

Basic

class sympy.core.basic.Basic

Base class for all objects in sympy.

Conventions:

1) When you want to access parameters of some instance, always use .args: Example:

>>> from sympy import symbols, cot
>>> from sympy.abc import x, y

>>> cot(x).args
(x,)

>>> cot(x).args[0]
x

>>> (x*y).args
(x, y)

>>> (x*y).args[1]
y

2) Never use internal methods or variables (the ones prefixed with “_”). Example:

>>> cot(x)._args    #don't use this, use cot(x).args instead
(x,)

args

Returns a tuple of arguments of ‘self’.

Example:

>>> from sympy import symbols, cot
>>> from sympy.abc import x, y

>>> cot(x).args
(x,)

>>> cot(x).args[0]
x

>>> (x*y).args
(x, y)

>>> (x*y).args[1]
y

Note for developers: Never use self._args, always use self.args. Only when you are creating your own new function, use _args in the __new__. Don’t override .args() from Basic (so that it’s easy to change the interface in the future if needed).

as_basic()

Converts polynomial to a valid sympy expression.

>>> from sympy import sin
>>> from sympy.abc import x, y

>>> p = (x**2 + x*y).as_poly(x, y)

>>> p.as_basic()
x*y + x**2

>>> f = sin(x)

>>> f.as_basic()
sin(x)

as_coeff_exponent(x)

c*x**e -> c,e where x can be any symbolic expression.

as_coefficient(expr)

Extracts symbolic coefficient at the given expression. In other words, this functions separates ‘self’ into product of ‘expr’ and ‘expr’-free coefficient. If such separation is not possible it will return None.

>>> from sympy import E, pi, sin, I
>>> from sympy.abc import x, y

>>> E.as_coefficient(E)
1
>>> (2*E).as_coefficient(E)
2

>>> (2*E + x).as_coefficient(E)
>>> (2*sin(E)*E).as_coefficient(E)

>>> (2*pi*I).as_coefficient(pi*I)
2

>>> (2*I).as_coefficient(pi*I)

as_independent(*deps)

Returns a pair with separated parts of a given expression independent of specified symbols in the first place and dependent on them in the other. Both parts are valid SymPy expressions.

>>> from sympy import sin, cos
>>> from sympy.abc import x, y

>>> (2*x*sin(x)+y+x).as_independent(x)
(y, x + 2*x*sin(x))

>>> (x*sin(x)*cos(y)).as_independent(x)
(cos(y), x*sin(x))

All other expressions are multiplicative:

>>> (sin(x)).as_independent(x)
(1, sin(x))

>>> (sin(x)).as_independent(y)
(sin(x), 1)

as_leading_term(*args, **kw_args)

Returns the leading term.

Example:

>>> from sympy.abc import x
>>> (1+x+x**2).as_leading_term(x)
1
>>> (1/x**2+x+x**2).as_leading_term(x)
x**(-2)

Note:

self is assumed to be the result returned by Basic.series().

as_numer_denom()

a/b -> a,b

The following is a possible way to modify Eq which are now just returned as (Eq(), 1). It is not a trivial change, however, and it causes many failures.

from sympy.core.relational import Equality from sympy import Eq if isinstance(self, Equality):

l = Symbol(‘l’, dummy=True) r = Symbol(‘r’, dummy=True) n, d = (l*self.lhs - r*self.rhs).as_numer_denom() return Eq(n.subs({l: 1, r: 0}),

n.subs({l: 0, r: -1})), d.subs({l: 1, r: 1})

as_poly(*symbols, **flags)

Converts ‘self’ to a polynomial or returns None.

When constructing a polynomial an exception will be raised in case the input expression is not convertible to a polynomial. There are situations when it is easier (simpler or prettier) to receive None on failure.

If no symbols were given and ‘self’ isn’t already a polynomial then all available symbols will be collected and used to form a new polynomial.

>>> from sympy import Poly, sin
>>> from sympy.abc import x, y

>>> print (x**2 + x*y).as_poly()
Poly(x**2 + x*y, x, y)

>>> print (x**2 + x*y).as_poly(x, y)
Poly(x**2 + x*y, x, y)

>>> print (x**2 + sin(y)).as_poly(x, y)
None

as_real_imag()

Performs complex expansion on ‘self’ and returns a tuple containing collected both real and imaginary parts. This method can’t be confused with re() and im() functions, which does not perform complex expansion at evaluation.

However it is possible to expand both re() and im() functions and get exactly the same results as with a single call to this function.

>>> from sympy import symbols, I

>>> x, y = symbols('xy', real=True)

>>> (x + y*I).as_real_imag()
(x, y)

>>> from sympy.abc import z, w

>>> (z + w*I).as_real_imag()
(-im(w) + re(z), im(z) + re(w))

assumptions0

Return object 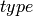assumptions.

For example:

Symbol(‘x’, real=True) Symbol(‘x’, integer=True)

are different objects. In other words, besides Python type (Symbol in this case), the initial assumptions are also forming their typeinfo.

Example:

>>> from sympy import Symbol
>>> from sympy.abc import x
>>> x.assumptions0
{}
>>> x = Symbol("x", positive=True)
>>> x.assumptions0
{'commutative': True, 'complex': True, 'imaginary': False,
'negative': False, 'nonnegative': True, 'nonpositive': False,
'nonzero': True, 'positive': True, 'real': True, 'zero': False}

atoms(*types)

Returns the atoms that form the current object.

By default, only objects that are truly atomic and can’t be divided into smaller pieces are returned: symbols, numbers, and number symbols like I and pi. It is possible to request atoms of any type, however, as demonstrated below.

Examples:

>>> from sympy import I, pi, sin
>>> from sympy.abc import x, y
>>> list((1+x+2*sin(y+I*pi)).atoms())

[y, I, 2, x, 1, pi]

If one or more types are given, the results will contain only those types of atoms:

Examples:

>>> from sympy import Number, NumberSymbol, Symbol
>>> sorted((1+x+2*sin(y+I*pi)).atoms(Symbol))

[x, y]

>>> sorted((1+x+2*sin(y+I*pi)).atoms(Number))
[1, 2]

>>> sorted((1+x+2*sin(y+I*pi)).atoms(Number, NumberSymbol))
[1, 2, pi]

>>> sorted((1+x+2*sin(y+I*pi)).atoms(Number, NumberSymbol, I))
[1, 2, pi, I]

Note that I (imaginary unit) and zoo (complex infinity) are special types of number symbols and are not part of the NumberSymbol class.

The type can be given implicitly, too:

>>> sorted((1+x+2*sin(y+I*pi)).atoms(x)) # x is a Symbol

[x, y]

Be careful to check your assumptions when using the implicit option since S(1).is_Integer = True but type(S(1)) is One, a special type of sympy atom, while type(S(2)) is type Integer and will find all integers in an expression:

>>> from sympy import S
>>> sorted((1+x+2*sin(y+I*pi)).atoms(S(1)))

[1]

>>> sorted((1+x+2*sin(y+I*pi)).atoms(S(2)))
[1, 2]

Finally, arguments to atoms() can select more than atomic atoms: any sympy type (loaded in core/__init__.py) can be listed as an argument and those types of “atoms” as found in scanning the arguments of the expression nonrecursively:

>>> from sympy import Function, Mul
>>> sorted((1+x+2*sin(y+I*pi)).atoms(Function))

[sin(y + pi*I)]

>>> sorted((1+x+2*sin(y+I*pi)).atoms(Mul))
[2*sin(y + pi*I)]

coeff(x, expand=True)

Returns the coefficient of the term “x” or None if there is no “x”.

Optional expand keyword argument allows one to control whether the expression is expanded before terms are collected, which can be useful if the term “x” isn’t nested inside of terms and you don’t want the returned coefficient to be expanded.

Example:

>>> from sympy import symbols
>>> from sympy.abc import x, y, z
>>> (3+2*x+4*x**2).coeff(1)
>>> (3+2*x+4*x**2).coeff(x)
2
>>> (3+2*x+4*x**2).coeff(x**2)
4
>>> (3+2*x+4*x**2).coeff(x**3)
>>> (z*(x+y)**2).coeff(z)
2*x*y + x**2 + y**2
>>> (z*(x+y)**2).coeff(z, expand=False)
(x + y)**2
>>>

compare(other)

Return -1,0,1 if the object is smaller, equal, or greater than other.

Not in the mathematical sense. If the object is of a different type from the “other” then their classes are ordered according to the sorted_classes list.

Example:

>>> from sympy.abc import x, y
>>> x.compare(y)
-1
>>> x.compare(x)
0
>>> y.compare(x)
1

static compare_pretty(a, b)

Is a > b in the sense of ordering in printing?

yes ..... return 1 no ...... return -1 equal ... return 0

Strategy:

It uses Basic.compare as a fallback, but improves it in many cases, like x**3, x**4, O(x**3) etc. In those simple cases, it just parses the expression and returns the “sane” ordering such as:

1 < x < x**2 < x**3 < O(x**4) etc.

Example:

>>> from sympy.abc import x
>>> from sympy import Basic
>>> Basic._compare_pretty(x, x**2)
-1
>>> Basic._compare_pretty(x**2, x**2)
0
>>> Basic._compare_pretty(x**3, x**2)
1

could_extract_minus_sign()

Canonical way to choose an element in the set {e, -e} where e is any expression. If the canonical element is e, we have e.could_extract_minus_sign() == True, else e.could_extract_minus_sign() == False.

For any expression, the set {e.could_extract_minus_sign(), (-e).could_extract_minus_sign()} must be {True, False}.

>>> from sympy.abc import x, y
>>> (x-y).could_extract_minus_sign() != (y-x).could_extract_minus_sign()
True

count_ops(*args, **kw_args)

Return the number of operations in expressions.

Examples: >>> from sympy.abc import a, b, x >>> from sympy import sin >>> (1+a+b**2).count_ops() POW + 2*ADD >>> (sin(x)*x+sin(x)**2).count_ops() 2 + ADD + MUL + POW

doit(**hints)

Evaluate objects that are not evaluated by default like limits, integrals, sums and products. All objects of this kind will be evaluated recursively, unless some species were excluded via ‘hints’ or unless the ‘deep’ hint was set to ‘False’.

>>> from sympy import Integral
>>> from sympy.abc import x, y

>>> 2*Integral(x, x)
2*Integral(x, x)

>>> (2*Integral(x, x)).doit()
x**2

>>> (2*Integral(x, x)).doit(deep = False)
2*Integral(x, x)

evalf(x, n=15, **options)

Evaluate the given formula to an accuracy of n digits. Optional keyword arguments:

subs=<dict>

Substitute numerical values for symbols, e.g. subs={x:3, y:1+pi}.

maxprec=N

Allow a maximum temporary working precision of N digits (default=100)

chop=<bool>

Replace tiny real or imaginary parts in subresults by exact zeros (default=False)

strict=<bool>

Raise PrecisionExhausted if any subresult fails to evaluate to full accuracy, given the available maxprec (default=False)

quad=<str>

Choose algorithm for numerical quadrature. By default, tanh-sinh quadrature is used. For oscillatory integrals on an infinite interval, try quad=’osc’.

verbose=<bool>

Print debug information (default=False)

expand(deep=True, power_base=True, power_exp=True, mul=True, log=True, multinomial=True, basic=True, **hints)

Expand an expression using hints.

See the docstring in function.expand for more information.

extract_additively(c)

Return None if it’s not possible to make self in the form something + c in a nice way, i.e. preserving the properties of arguments of self.

>>> from sympy import symbols

>>> x, y = symbols('xy', real=True)

>>> ((x*y)**3).extract_additively(1)

>>> (x+1).extract_additively(x)
1

>>> (x+1).extract_additively(2*x)

>>> (x+1).extract_additively(-x)
1 + 2*x

>>> (-x+1).extract_additively(2*x)
1 - 3*x

extract_multiplicatively(c)

Return None if it’s not possible to make self in the form c * something in a nice way, i.e. preserving the properties of arguments of self.

>>> from sympy import symbols, Rational

>>> x, y = symbols('xy', real=True)

>>> ((x*y)**3).extract_multiplicatively(x**2 * y)
x*y**2

>>> ((x*y)**3).extract_multiplicatively(x**4 * y)

>>> (2*x).extract_multiplicatively(2)
x

>>> (2*x).extract_multiplicatively(3)

>>> (Rational(1,2)*x).extract_multiplicatively(3)
x/6

func

The top-level function in an expression.

The following should hold for all objects:

>> x == x.func(*x.args)

Example:

>>> from sympy.abc import x
>>> a = 2*x
>>> a.func
<class 'sympy.core.mul.Mul'>
>>> a.args
(2, x)
>>> a.func(*a.args)
2*x
>>> a == a.func(*a.args)
True

getO(e)

Returns the O(..) symbol, or None if there is none.

has(*patterns)

Return True if self has any of the patterns.

Example: >>> from sympy.abc import x >>> (2*x).has(x) True >>> (2*x/x).has(x) False

has_all_symbols(*args, **kw_args)

Return True if ‘self’ has all of the symbols.

>>> from sympy import sin
>>> from sympy.abc import x, y, z

>>> (x**2 + sin(x*y)).has_all_symbols(x, y)
True

>>> (x**2 + sin(x*y)).has_all_symbols(x, y, z)
False

has_any_symbols(*args, **kw_args)

Return True if ‘self’ has any of the symbols.

>>> from sympy import sin
>>> from sympy.abc import x, y, z

>>> (x**2 + sin(x*y)).has_any_symbols(z)
False

>>> (x**2 + sin(x*y)).has_any_symbols(x, y)
True

>>> (x**2 + sin(x*y)).has_any_symbols(x, y, z)
True

has_piecewise

Returns True if any args are Piecewise or has_piecewise

is_number

Returns True if ‘self’ is a number.

>>> from sympy import log
>>> from sympy.abc import x, y

>>> x.is_number
False
>>> (2*x).is_number
False
>>> (2 + log(2)).is_number
True

is_rational_function(*syms)

Test whether function is rational function - ratio of two polynomials. When no arguments are present, Basic.atoms(Symbol) is used instead.

Example:

>>> from sympy import symbols, sin
>>> from sympy.abc import x, y

>>> (x/y).is_rational_function()
True

>>> (x**2).is_rational_function()
True

>>> (x/sin(y)).is_rational_function(y)
False

iter_basic_args()

Iterates arguments of ‘self’.

Example:

>>> from sympy.abc import x
>>> a = 2*x
>>> a.iter_basic_args()
<tupleiterator object at 0x...>
>>> list(a.iter_basic_args())
[2, x]

leadterm(x)

Returns the leading term a*x**b as a tuple (a, b).

Example:

>>> from sympy.abc import x
>>> (1+x+x**2).leadterm(x)
(1, 0)
>>> (1/x**2+x+x**2).leadterm(x)
(1, -2)

Note:

self is assumed to be the result returned by Basic.series().

limit(x, xlim, direction='+')

Compute limit x->xlim.

lseries(x, x0)

lseries is a generator yielding terms in the series.

Example: if you do:

for term in sin(x).lseries(x, 0):

print term

It will print all terms of the sin(x) series (i.e. it never terminates).

The advantage of lseries() over nseries() is that many times you are just interested in the next term in the series (i.e. the first term for example), but you don’t know how many you should ask for in nseries() using the “n” parameter.

See also nseries().

match(pattern)

Pattern matching.

Wild symbols match all.

Return None when expression (self) does not match with pattern. Otherwise return a dictionary such that

pattern.subs(self.match(pattern)) == self

Example:

>>> from sympy import symbols, Wild
>>> from sympy.abc import x, y
>>> p = Wild("p")
>>> q = Wild("q")
>>> r = Wild("r")
>>> e = (x+y)**(x+y)
>>> e.match(p**p)
{p_: x + y}
>>> e.match(p**q)
{p_: x + y, q_: x + y}
>>> e = (2*x)**2
>>> e.match(p*q**r)
{p_: 4, q_: x, r_: 2}
>>> (p*q**r).subs(e.match(p*q**r))
4*x**2

matches(expr, repl_dict={}, evaluate=False)

Helper method for match() - switches the pattern and expr.

Can be used to solve linear equations:

>>> from sympy import Symbol, Wild, Integer
>>> a,b = map(Symbol, 'ab')
>>> x = Wild('x')
>>> (a+b*x).matches(Integer(0))
{x_: -a/b}

n(x, n=15, **options)

Evaluate the given formula to an accuracy of n digits. Optional keyword arguments:

subs=<dict>

Substitute numerical values for symbols, e.g. subs={x:3, y:1+pi}.

maxprec=N

Allow a maximum temporary working precision of N digits (default=100)

chop=<bool>

Replace tiny real or imaginary parts in subresults by exact zeros (default=False)

strict=<bool>

Raise PrecisionExhausted if any subresult fails to evaluate to full accuracy, given the available maxprec (default=False)

quad=<str>

Choose algorithm for numerical quadrature. By default, tanh-sinh quadrature is used. For oscillatory integrals on an infinite interval, try quad=’osc’.

verbose=<bool>

Print debug information (default=False)

new(*args)

Create new ‘similar’ object.

this is conceptually equivalent to:

type(self) (*args)

but takes type assumptions into account. See also: assumptions0

Example:

>>> from sympy.abc import x
>>> x.new("x")
x

nseries(x, x0, n)

Calculates a generalized series expansion.

nseries calculates “n” terms in the innermost expressions and then builds up the final series just by “cross-multiplying” everything out.

Advantage – it’s fast, because we don’t have to determine how many terms we need to calculate in advance.

Disadvantage – you may end up with less terms than you may have expected, but the O(x**n) term appended will always be correct and so the result, though perhaps shorter, will also be correct.

See also lseries().

removeO()

Removes the O(..) symbol if there is one

rewrite(*args, **hints)

Rewrites expression containing applications of functions of one kind in terms of functions of different kind. For example you can rewrite trigonometric functions as complex exponentials or combinatorial functions as gamma function.

As a pattern this function accepts a list of functions to to rewrite (instances of DefinedFunction class). As rule you can use string or a destination function instance (in this case rewrite() will use the str() function).

There is also possibility to pass hints on how to rewrite the given expressions. For now there is only one such hint defined called ‘deep’. When ‘deep’ is set to False it will forbid functions to rewrite their contents.

>>> from sympy import sin, exp, I
>>> from sympy.abc import x, y

>>> sin(x).rewrite(sin, exp)
-I*(exp(I*x) - exp(-I*x))/2

series(x, point=0, n=6, dir='+')

Series expansion of “self” around “point”.

Usage:

Returns the Taylor (Laurent or generalized) series of “self” around the point “point” (default 0) with respect to “x” until the n-th term (default n is 6).

For dir=”+” (default) it calculates the series from the right and for dir=”-” the series from the left. For smooth functions this argument doesn’t matter.

Notes:

This method is the most high level method and it returns the series including the O(x**n) term.

Internally, it executes a method nseries(), see nseries() docstring for more information.

solve4linearsymbol(eqn, rhs, symbols=None)

Solve equation “eqn == rhs” with respect to some linear symbol in eqn.

Returns (symbol, solution). If eqn is nonlinear with respect to all symbols, then return trivial solution (eqn, rhs).

subs(*args)

Substitutes an expression.

Calls either _subs_old_new, _subs_dict or _subs_list depending if you give it two arguments (old, new), a dictionary or a list.

Examples:

>>> from sympy import pi
>>> from sympy.abc import x, y
>>> (1+x*y).subs(x, pi)
1 + pi*y
>>> (1+x*y).subs({x:pi, y:2})
1 + 2*pi
>>> (1+x*y).subs([(x,pi), (y,2)])
1 + 2*pi

Symbol

class sympy.core.symbol.Symbol

Assumptions::

real = True commutative = True

You can override the default assumptions in the constructor::

>>> from sympy import symbols
>>> A,B = symbols('AB', commutative = False)
>>> bool(A*B != B*A)
True
>>> bool(A*B*2 == 2*A*B) == True # multiplication by scalars is commutative
True

Add

class sympy.core.add.Add

extract_leading_order(*args, **kw_args)

Returns the leading term and it’s order.

Examples:

>>> from sympy.abc import x
>>> (x+1+1/x**5).extract_leading_order(x)
((x**(-5), O(x**(-5))),)
>>> (1+x).extract_leading_order(x)
((1, O(1)),)
>>> (x+x**2).extract_leading_order(x)
((x, O(x)),)

classmethod flatten(seq)

Takes the sequence “seq” of nested Adds and returns a flatten list.

Returns: (commutative_part, noncommutative_part, order_symbols)

Applies associativity, all terms are commutable with respect to addition.

matches(expr, repl_dict={}, evaluate=False)

Matches Add/Mul “pattern” to an expression “expr”.

repl_dict ... a dictionary of (wild: expression) pairs, that get

returned with the results

evaluate .... if True, then repl_dict is first substituted into the

pattern, and then _matches_commutative is run

This function is the main workhorse for Add/Mul.

For instance:

>> from sympy import symbols, Wild, sin >> a = Wild(“a”) >> b = Wild(“b”) >> c = Wild(“c”) >> x, y, z = symbols(“x y z”) >> (a+b*c)._matches_commutative(x+y*z) {a_: x, b_: y, c_: z}

In the example above, “a+b*c” is the pattern, and “x+y*z” is the expression. Some more examples:

>> (a+b*c)._matches_commutative(sin(x)+y*z) {a_: sin(x), b_: y, c_: z} >> (a+sin(b)*c)._matches_commutative(x+sin(y)*z) {a_: x, b_: y, c_: z}

The repl_dict contains parts, that were already matched, and the “evaluate=True” kwarg tells _matches_commutative to substitute this repl_dict into pattern. For example here:

>> (a+b*c)._matches_commutative(x+y*z, repl_dict={a: x}, evaluate=True) {a_: x, b_: y, c_: z}

_matches_commutative substitutes “x” for “a” in the pattern and calls itself again with the new pattern “x+b*c” and evaluate=False (default):

>> (x+b*c)._matches_commutative(x+y*z, repl_dict={a: x}) {a_: x, b_: y, c_: z}

the only function of the repl_dict now is just to return it in the result, e.g. if you omit it:

>> (x+b*c)._matches_commutative(x+y*z) {b_: y, c_: z}

the “a: x” is not returned in the result, but otherwise it is equivalent.

Set

class sympy.core.sets.Set

Represents any kind of set.

Real intervals are represented by the Interval class and unions of sets by the Union class. The empty set is represented by the EmptySet class and available as a singleton as S.EmptySet.

complement

The complement of ‘self’.

As a shortcut it is possible to use the ‘~’ or ‘-‘ operators:

>>> ##

>>> Interval(0, 1).complement
Union((-oo, 0), (1, oo))
>>> ~Interval(0, 1)
Union((-oo, 0), (1, oo))
>>> -Interval(0, 1)
Union((-oo, 0), (1, oo))

contains(other)

Returns True if ‘other’ is contained in ‘self’ as an element.

As a shortcut it is possible to use the ‘in’ operator:

>>> from sympy import Interval

>>> Interval(0, 1).contains(0.5)
True
>>> 0.5 in Interval(0, 1)
True

inf

The infimum of ‘self’.

>>> ##

>>> Interval(0, 1).inf
0
>>> Union(Interval(0, 1), Interval(2, 3)).inf
0

intersect(other)

Returns the intersection of ‘self’ and ‘other’.

>>> from sympy import Interval

>>> Interval(1, 3).intersect(Interval(1, 2))
[1, 2]

measure

The (Lebesgue) measure of ‘self’.

>>> ##

>>> Interval(0, 1).measure
1
>>> Union(Interval(0, 1), Interval(2, 3)).measure
2

subset(other)

Returns True if ‘other’ is a subset of ‘self’.

>>> from sympy import Interval

>>> Interval(0, 1).contains(0)
True
>>> Interval(0, 1, left_open=True).contains(0)
False

sup

The supremum of ‘self’.

>>> ##

>>> Interval(0, 1).sup
1
>>> Union(Interval(0, 1), Interval(2, 3)).sup
3

union(other)

Returns the union of ‘self’ and ‘other’. As a shortcut it is possible to use the ‘+’ operator:

>>> from sympy import Interval

>>> Interval(0, 1).union(Interval(2, 3))
Union([0, 1], [2, 3])
>>> Interval(0, 1) + Interval(2, 3)
Union([0, 1], [2, 3])

Similarly it is possible to use the ‘-‘ operator for set differences:

>>> Interval(0, 2) - Interval(0, 1)
(1, 2]

Interval

class sympy.core.sets.Interval

Represents a real interval as a Set.

Usage:

Returns an interval with end points “start” and “end”.

For left_open=True (default left_open is False) the interval will be open on the left. Similarly, for right_open=True the interval will be open on the right.

Examples:

>>> from sympy import Symbol, Interval, sets

>>> Interval(0, 1)
[0, 1]
>>> Interval(0, 1, False, True)
[0, 1)

>>> a = Symbol('a', real=True)
>>> Interval(0, a)
[0, a]

Notes:

• Only real end points are supported
• Interval(a, b) with a > b will return the empty set
• Use the evalf() method to turn an Interval into an mpmath ‘mpi’ interval instance

end

The right end point of ‘self’. This property takes the same value as the ‘sup’ property.

>>> ##

>>> Interval(0, 1).end
1

left_open

True if ‘self’ is left-open.

>>> ##

>>> Interval(0, 1, left_open=True).left_open
True
>>> Interval(0, 1, left_open=False).left_open
False

right_open

True if ‘self’ is right-open.

>>> ##

>>> Interval(0, 1, right_open=True).right_open
True
>>> Interval(0, 1, right_open=False).right_open
False

start

The left end point of ‘self’. This property takes the same value as the ‘inf’ property.

>>> ##

>>> Interval(0, 1).start
0

Union

class sympy.core.sets.Union

Represents a union of sets as a Set.

Examples:

>>> from sympy import Union, Interval

>>> Union(Interval(1, 2), Interval(3, 4))
Union([1, 2], [3, 4])

The Union constructor will always try to merge overlapping intervals, if possible. For example:

>>> Union(Interval(1, 2), Interval(2, 3))
[1, 3]