En este post se analiza la velocidad de escape de un cuerpo masivo desde el punto de vista relativista en el espacio de Minkowski en un folio espacial donde se usa el tiempo cronológico y no el tiempo propio. Para ello se parte del lagrangiano relativista (1) de una partícula con masa propia (m_0) sometida a la acción de la gravedad de un cuerpo masivo con longitud gravitacional definida en un post anterior. De (1) se halla el hamiltoniano relativista (2) dicho hamiltoniano es independiente del tiempo por lo que no solo se conserva, sino que su valor vale la energía mecánica total del cuerpo. Como la lagrangiana no depende del ángulo (en coordenadas polares ya que se mueve en el plano eclíptico), entonces el momento canónico que es el momento areolar se conserva (3), luego se halla la velocidad radial (5) y de la condición que dicha velocidad se anula para distancias muy alejadas se encuentra el resultado que el hamiltoniano debe anularse en toda la órbita. De aplicar las condiciones iniciales se halla que el valor del módulo de la velocidad de escape es (6). Se puede verificar la coherencia a baja velocidad del resultado, pero a diferencia de lo que ocurre en la visión no relativista, la velocidad de escape es la de la luz en el caso que el radio del grave tienda a cero. Desde este punto de vista es coherente cuando se dice que la masa de un agujero negro se reduce a una singularidad donde ni la luz puede escapar.
Archivo por meses: septiembre 2010
Gravitational length
La longitud gravitacional es un término poco enunciado en relatividad y mecánica newtoniana. Se la define como (1) y ella está relacionada con la máxima velocidad de escape. La velocidad de escape desde un punto de vista no relativista viene dada por (2). Operando se la puede llevar a una forma más operacional (4). Donde de las dos situaciones límites:
- Es un casquete estático sin rotación
- Es un casquete con la máxima velocidad tangencial en el ecuador
En el peor de los casos basta un radio del objeto masivo menor a dos veces la longitud gravitacional para que la velocidad de escape sea mayor a la luz.
Oblique shot in special relativity, 特殊相対性理論
Si bien existe mucha bibliografía sobre tiro oblicuo a modulo de gravedad constante a baja velocidad, muy poco se ha escrito sobre el tema cuando las velocidades son relativistas y la gravedad es lo suficientemente grande como para evitar que se escape. En este tipo de situaciones la trayectoria no es más una parábola sino un arco de hipérbola. Una forma sencilla de encarar el problema es partiendo de las ecuaciones dinámicas con masa relativista. Esto permite usar el tiempo cronológico como parámetro y no el tiempo propio. Resolviendo las ecuaciones dinámicas e imponiendo las condiciones iniciales para la velocidad se obtienen las constantes (1) que forman parte de las ecuaciones de la velocidad en coordenadas cartesianas (2). Cabe destacar que a alta velocidades la geometría del espacio de Minkowski no es válido el concepto de independencia de movimientos como ocurre en la vida cotidiana (3) pues la proyección de la velocidad en el eje x depende de la proyección de la velocidad en el eje y. Se recupera lo ya conocido cuando las velocidades son bajas (4). Partiendo de condiciones nulas para la posición inicial se puede hallar el alcance (R) y la altura máxima (H) integrando (2) en el tiempo cronológico. Donde es simple mostrar que se recuperan los resultados clásico para bajas velocidades.
Un estudio detallado se encuentra en el item «Tiro oblicuo en Relatividad Especial» en en wiki de apoyo.
|
|
The Fermi-Walker transported in E.R. 一般相対性理論
En el espacio de Minkowski un observador comovil con un sistema acelerado puede representarse como una rotación en dicho espacio, entonces la ecuación que rige el movimiento comovil vendría dada por (1). Donde la representación matricial del operador en una carta euclidea sería antisimétrica. Además dicho operdor no debe afectar a los vectores espaciales pues esto podría tener efecto de anticausalidad indeseables, esto se traduce por la condición (2). Una forma covariante de definir dicho operador es por el producto exterior (3′), que no debe confundirse con el producto vectorial. Entonces a dicho operador es el que se conoce como transporte de Fermi-Walker. Es fácil verificar que dicha definición devuleve el resultado deseado (4).
E.R. accelerated comoving system, 一般相対性理論
En este caso se analiza en el espacio de Minkowski como describir un sistema comovil con un sistema acelerado. Una forma de cambio coordenado es dado por (1), (2), (3), (4). El cuál cumple la condición de ortogonalidad. En el caso de un sistema comovil con un objeto en caída libre (movimiento hiperbólico), el cambio coordenado es el que se muestra en la parte inferior de la figura.
Hyperbolic motion in general relativity, 一般相対性理論
El movimiento hiperbólico aparece cuando se estudia el movimiento de un cuerpo sometido a fuerza constante, pero en el caso de un cuerpo libremente gravitante, corresponde al caso de caída libre. Aquí se resuelve el problema en el espacio de Minkowski. (1) y (2) son la propiedades de la cudri-velocidad y la cuadri-aceleración. Por otro lado (5) indica que la aceleración en módulo debe ser igual a la gravedad debido al principio de equivalencia débil entre la masa inercial y la gravitatória. Operando algebráicamente resulta el sistema de ecuaciones (6) y (7) cuya solución es (8) y (9). Se toma como condición inicial de que el tiempo propio coincida con el cronológico del sistema inercial. Luego para tener en cuenta que parte desde el origen y se lo deja caer se efectúa un conveniente cambio de variable, eliminando la parametrización queda (10), ó (11) que da la ecuación de movimiento. Cabe destacar que este resultado coincide con lo conocido para campos débiles (12).
Una explicación más detallada puede verse en la sección Movimiento Hiperbólico de mi wiki.
Sistemas inerciales, punto de vista amplio
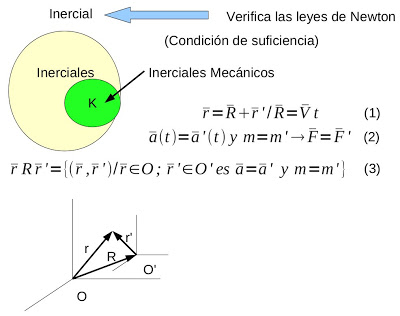
En general se confunde como condición de necesidad y suficiencia que un sistema inercial es aquel que verifique las leyes de Newton. Pero esto dejaría afuera a los sistemas inerciales de la relatividad restringida y otros que pudieran aparecer. Para subsanar este inconveniente se propone la condición de suficiencia:
Sistema es inercial <= Verifica las leyes de Newton
Como se parecia en la figura esta condición permite restringir a un subconjunto K conocido como sistemas inerciales mecánicos. En dichos sistemas la transformaciones de Galileo (1) (donde V=cte) permiten verificar la invariancia de la aceleración para ambos sistemas de referencia O y O’. Junto con la invariancia de la masa (hipótesis Ad-Hoc) resulta en la invariancia de las leyes de Newton (2). (2) permite construir una relación de equivalencia entre sistemas dinámicos inerciales (3) de manera tal que K/R forman una partición de dicho conjunto.
Una versión extendida puede verse en el wiki: Sistemas Inerciales .
Cinemática en Curvas
ver: Cinemática en Curvas.
Donde hago una descripción del punto de vista intrínseco y extrínseco.