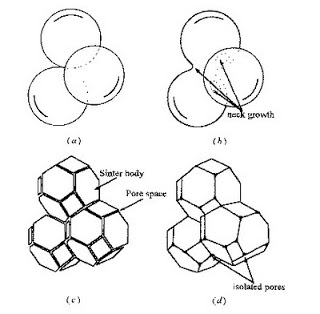
En el wiki he publicado un apunte sobre el sinterizado de plovos y fenómenos de superficie.
Archivo por meses: julio 2010
Pearson’s Unimodal curves
 |
| De blog2 |
Las curvas unimodales de Pearson tiene su utilidad en ajustar un histograma de frecuencias relativas hallado de manera experimental a algún tipo de curva teórica conocida, la cual es solución de la ecuación (1). Los momentos centrados enunciados en (2) cuando está referido a datos experimentales se debe reemplazar la integral por la sumatoria sin que varíe la ecuaciones (3), (4), (5) para hallar los coeficientes de la ecuación diferencial (1). El criterion (6) permite encuadrar los datos dentro de algún tipo de curva estudiada por Pearson. Las curvas del tipo I y II corresponde a la distribución gamma. Las curvas de tipo III coresponde la distribución de Euler.
Cabe destacar que basta con calcular hasta el momento de orden cuatro para hallar una gran variedad de distribuciones de probabilidad.
Fe de errata: En la fórmula (5) se refiere a b_2 no al coeficiente b_0.
Photons, chemical potential and curvature
 |
| De blog2 |
El gas de fotones en equilibrio con la materia es una de las cosas más estudiadas en universos euclídeos. Aqui doy una breve descripción del mismo sin apelar a usar la estadística de Bose-Einstein para justificar la ecuación de estado (1). Pues los fotones son en si bosones. Pero a diferncia del Helio, en los fotones no aparece los fenómenos de condesación.
Las dos propiedades interesantes que poseé un gas de fotones es la existencia de una entropía que me limita la energía usable de un haz luminoso (2), y la otra es que su potencial químico es nulo. Esto último indica que el gas siempre se mantiene como una sustancia pura. Ahora bien es bien conocido que el potencial químico en una interfaz no plana depende de la curvatura. Ahora bien en el caso de fotones en un medio interestelar no existe fenómenos de tensión superficial, por lo tanto esta dependencia debe estar relacionada (especulando) con la curvatura escalar (5) afectada de un signo menos (pues la curvatura es positiva). Esto lo hago para que en el caso de agujeros negros el potencial químico del gas en las vecindades al agujero sea lo bastante negativa para que favoresca la migración de fotones hacia el agujero negro.
Bell Inequality and False Realism
 |
| De blog2 |
Una de las mayores objeciones fue hecha por Einstein en su famosa publicación EPR. En la cuál da condiciones suficientes para que una propiedad física sea un elemento de la realidad. Una veintena de años más tarde Bell formula su famosa desigualdad que debe verificar cualquier sistema de codificación binaria (Este resultado es conocido como la desigualdad CHSH). El ella hay dos observadores Alicia y Beto que están lo sufientemente aislado uno del otro para no espiarse. Carlitos envía dos señales S1 a Alicia y S2 a Beto en cualquier momento del experimento sin que ellos lo sepan. Alicia tiene dos decodificadores Q y R que solo devuelde dos valores +1 y -1. Lo mismo Beto pero tiene los decodificadores S y T. Ellos tabulan los valores que reciben y cuando termina el experimento se reunen con Carlitos para evaluar el observable F (1) en el cuál tiene implicito el principio del 3º excluido que respeta la lógica clásica. Bell demuesta que el valor medio de F está acotado por (4).
Los experimentos de Aspect mostraron que si se toma como medio de trasporte el fotón y Q, R, S, T no da valores sino estados medibles del fotón, resulta (5) por lo tanto se viola la desigualdad de Bell. Pero porque ocurre esto, por tres motivos a tener en cuenta aún en el mundo macroscópico en que vivimos (se usaron fotones no electrones)
- En lógica cúantica no vale el principio del 3º excluido por lo tanto es un tipo de lógica multimodal.
- Asumir que Q, R, S, T dan valores deinidos y no estados. Esto es conocido como realismo.
- Suponer que lo que mide Alicia no está influenciado por lo que mide Beto aún si están lo suficientemente lejos de manera tal que la información debe viajar a velocidad mayor que la velocidad de la luz en el vacío. Esto es conocido como localidad.
Pero 1, 2, 3. También lo verifica si en lugar de usar fotones y su descripción cuántica, usamos ondas electromagnéticas transversales. Como lo demostraré en un futuro post.
Falacia de Autoridad en comunidades científicas
La falacia de autoridad (FA) o argumento de autoridad es un argumento falaz el cual es aceptado sin cuestionamientos porque así lo afirma una autoridad en la materia. Si cuestionar que las autoridades pueden tener sus falsas creencias.
Hay que hacer la salvedad en el caso de la enseñanza de las ciencias en el ámbito universitario donde se forma un recurso humano. Pues en dichos ámbitos debe existir una autoridad aceptada del docente y una credibilidad de sus dichos. En dichos ámbitos más que nunca vale el aforismo Magister dixit ó «el maestro lo dijo». En dicho aforismo subyace la autoridad como guía de conocimiento que procede de los maestros y la enseñanza tradicional.
Pero en ciencias hay situaciones y períodos de tiempos donde la FA cobra vigencia, pero a diferencia de cualquier disciplina dogmática, al ser públicos los resultados, son factibles de revisión y como consecuencia la falacia queda al descubierto. Pero modernamente como perduraría una FA, muy simple, con las editoriales científicas, donde cada vez menos científicos de países en vía de desarrollo accedan a dichas publicaciones. Ó que las publicaciones que cuestionan la falacia aparezcan en revistas de bajo impacto. También la FA ocurre en congresos donde el invitado extranjero es visto como un ídolo y nadie se anima a cuestionar sus dichos. Todo esto pone en tela de juicio el moderno sistema científico tanto mundial como nacional.
Hablemos de acá, de la Argentina, entre pares es donde más se ve la FA, no en los temas de ciencia en sí, sino en las políticas científicas, en los ámbitos académicos, etc. Donde el hecho de ser un investigador reconocido del CONICET da autoridad de opinar sobre cualquier cosa y decir cualquier barbaridad. Este status quo es no solo alimentado por los más viejos de la comunidad sino por los jóvenes que bajo un estado de panquequismo en un principio se revelan para luego aceptar mansamente las costumbres que promueven la FA, a tal punto de ser los principales obsecuentes.
Hay que hacer la salvedad en el caso de la enseñanza de las ciencias en el ámbito universitario donde se forma un recurso humano. Pues en dichos ámbitos debe existir una autoridad aceptada del docente y una credibilidad de sus dichos. En dichos ámbitos más que nunca vale el aforismo Magister dixit ó «el maestro lo dijo». En dicho aforismo subyace la autoridad como guía de conocimiento que procede de los maestros y la enseñanza tradicional.
Pero en ciencias hay situaciones y períodos de tiempos donde la FA cobra vigencia, pero a diferencia de cualquier disciplina dogmática, al ser públicos los resultados, son factibles de revisión y como consecuencia la falacia queda al descubierto. Pero modernamente como perduraría una FA, muy simple, con las editoriales científicas, donde cada vez menos científicos de países en vía de desarrollo accedan a dichas publicaciones. Ó que las publicaciones que cuestionan la falacia aparezcan en revistas de bajo impacto. También la FA ocurre en congresos donde el invitado extranjero es visto como un ídolo y nadie se anima a cuestionar sus dichos. Todo esto pone en tela de juicio el moderno sistema científico tanto mundial como nacional.
Hablemos de acá, de la Argentina, entre pares es donde más se ve la FA, no en los temas de ciencia en sí, sino en las políticas científicas, en los ámbitos académicos, etc. Donde el hecho de ser un investigador reconocido del CONICET da autoridad de opinar sobre cualquier cosa y decir cualquier barbaridad. Este status quo es no solo alimentado por los más viejos de la comunidad sino por los jóvenes que bajo un estado de panquequismo en un principio se revelan para luego aceptar mansamente las costumbres que promueven la FA, a tal punto de ser los principales obsecuentes.
DNA metric representation
 |
| De blog2 |
En esta entrega se muestra como poder representar una secuencia lineal de DNA perteneciente a un cromosoma en una suceción de puntos en un plano bidimensional por medio de (1) y (2). En este conjunto de puntos defino la distancia trivial (4), la cual permite definir cuando una secuencia es vecina a otra, y cuando una subsecuencia es trasnportable dentro de la misma secuencia (5). (3) permite general una representación binaria matricial de la secuencia que en si es una variante del chaos game representation.