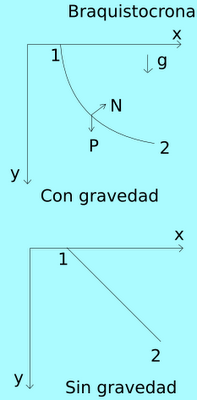
El problema de la braquistocrona es encontrar la curva sobre la cual el tiempo de caída entre dos puntos (1 y 2) sea el mínimo posible. El el caso de que no hubiera gravedad, dicha curva es la línea recta y coincide con la curva de menor distancia entre dos puntos, pero cuando hay gravedad no hay coincidencia. Esta falta de coincidencia es un indicativo de que el tiempo se ha curvado a causa de la presencia de un cuerpo masivo, como ser la Tierra. En el enlace:
https://sites.google.com/site/forodehoraciocastellini/fisica-basica/apuntes-de-clase/braquistocrona
hago una descripción de como calcular dicha curva por el método variacional clásico.
Archivo por meses: octubre 2010
Onda de acción y cuántica, 量子力学
Sea el lagrangiano (1) de una partícula masiva, luego el momento canónico conjugado vendrá dado por (2). En función de esto se puede hallar el hamiltoniano (3), el cual se supone independiente del tiempo (4), por lo que el sistema es autónomo. Bajo tales circunstancias el hamiltoniano es constante en la órbita y vale la energía mecánica total (5). Si se hace una transformación canónica (6) a una nueva hamiltoniana, K=0, (7), resulta que ahora en el nuevo espacio de las fases el momento es la canónica conjugada de la coordenada generalizada (8). A (9) se lo conoce como ecuación de Hamilton-Jacoby, cuya solución es la acción hamiltoniana (10), donde los nuevos momentos P son las condiciones iniciales (11). Es fácil comprobar que además el hamiltoniano es ahora la canónica conjugada del tiempo en un espacio de las fases extendido (12). La acción cuando se verifica (4) es (13). S(q,t)=cte es similar a la ecuación de un frente de onda donde su vector de onda (14) no es otra cosa que el momento canónico. Luego de la teoría de ondas la velocidad de grupo es (14-bis) (segundo 14), si se compara este resultado con el caso de un fotón es sorprendente la coincidencia, pero acá no corresponde al caso de una partícula libre. La onda de acción es 15 que corresponde a una función de onda escalar donde tiene sentido su módulo al cuadrado que corresponde a la probabilidad condicional de hallar la partícula en un estado dado.
Observación: No se debe confundir el momento canónico con el operador momento (16).
The harmonic oscillator in Einstein’s relativity
En la figura superior se puede ver como el hamiltoniano relativista (1) de una partícula genera curvas cerradas que corresponde a las oscilaciones donde la carta local es la cronológica sin curvatura causada por la materia. Para hallar como afecta esto en la frecuencia de oscilación haré uso de la teoría de Hamilton-Jacoby. Primeramente se despeja el momento generalizado (2) donde H_0 es el valor de la energía inicial. Para luego hallar la función principal de Hamilton (3) para encontrar la variable angular de acción (4). Acá se puede hacer dos aproximaciones dada la complejidad de la integral elíptica involucrada. Una es suponer una situación cuasi-relativista de tal manera de aproximar dicha integral por funciones gamma. Lo que resulta finalmente que la variable angular de acción es (5) función implícita del hamiltoniano, luego en función de esto se puede hallar la frecuencia angular (6) donde se aprecia que depende de la energía inicial. Además cuanto mayor sea esta tanto mas largo es el período, pero en el caso ultra relativista (7) toma un valor mínimo.